|
Выпуск 6. Полиномиальные тренды
Напомним, что в общем случае
временной ряд представляется соотношением 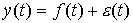 [8], где [8], где 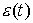 - случайная
составляющая, - случайная
составляющая, 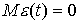 . В случае полиномиального тренда временной ряд
представляется в виде: . В случае полиномиального тренда временной ряд
представляется в виде: 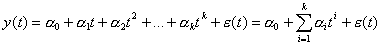 . .
Перепишем последнее соотношение в таком виде: 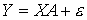 , где матрица , где матрица  , ,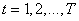 .Обозначим .Обозначим 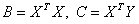 ,
где значок ,
где значок 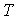 - обозначает транспонирование. Тогда - обозначает транспонирование. Тогда 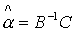 . Вычислим . Вычислим 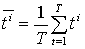 , и тогда , и тогда  , где , где 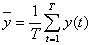 . Точечная оценка прогноза . Точечная оценка прогноза 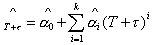 . Зачастую ее точность ожидает желать лучшего. Тогда актуальным
есть использование интервального прогноза . Зачастую ее точность ожидает желать лучшего. Тогда актуальным
есть использование интервального прогноза 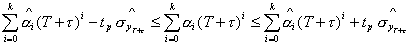 , где , где
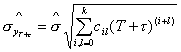 , , 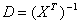 , , 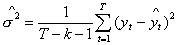 , ,
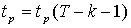 - доверительная граница распределения Стьюдента с - доверительная граница распределения Стьюдента с 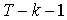 степенями свободы,
соответствующий уровню значимости степенями свободы,
соответствующий уровню значимости 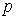 . .
Как было указано в выпуске 5 , эволюторно
изменяющаяся долговременная составляющая достаточно хорошо представима рядом
Тейлора., следовательно, именно эта составляющая во многих случаях может
рассматриваться как полиномиальный тренд.
Рассмотрим пример. Пусть
исходные данные представлены в таблице.
|
t
|
1
|
2
|
3
|
4
|
5
|
|
Y
|
2
|
5
|
-5
|
-9
|
-20
|
Предположим, что они представимы полиномом третьего
порядка. Тогда матрица 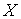 имеет вид: имеет вид:
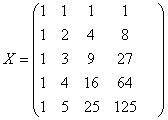 , , 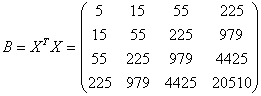 , ,
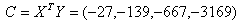 . .
Решаем уравнение 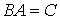 ,
например, методом Гаусса. Получим ,
например, методом Гаусса. Получим
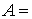 (-37/5, 108/7, -85/14, 1/2), временной ряд имеет вид (-37/5, 108/7, -85/14, 1/2), временной ряд имеет вид
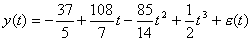 . Рассчитанные значения приведены в таблице. . Рассчитанные значения приведены в таблице.
|
|
|
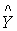
|
|
1
|
2
|
2.457
|
|
2
|
5
|
3.171
|
|
3
|
-5
|
-2.257
|
|
4
|
-9
|
-10.829
|
|
5
|
-20
|
-19.543
|
Доверительная граница распределения Стьюдента 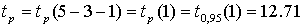 . .
Найдем 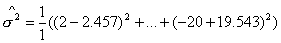 =14.63, =14.63, 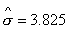 . Обратная матрица . Обратная матрица 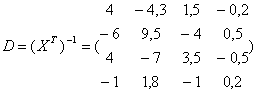 . Считаем, что прогноз необходим на один период,
следовательно . Считаем, что прогноз необходим на один период,
следовательно 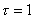 . Рассчитаем . Рассчитаем  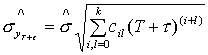 =1156. =1156.
Точечный прогноз 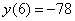 . .
Интервальный прогноз 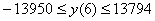 . Интервал получился ну очень большим, что свидетельствует о
низком качестве полученной зависимости, что объясняется малым количеством точек
наблюдения и сравнительно большим количеством членов полинома. . Интервал получился ну очень большим, что свидетельствует о
низком качестве полученной зависимости, что объясняется малым количеством точек
наблюдения и сравнительно большим количеством членов полинома.
|


 ,
,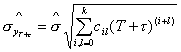 ,
, 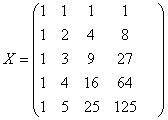 ,
, 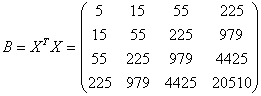
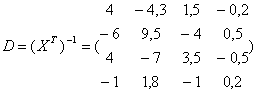 . Считаем, что прогноз необходим на один период,
следовательно
. Считаем, что прогноз необходим на один период,
следовательно 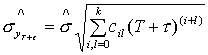 =1156.
=1156.